بسم الله الرحمن الرحیم
با سلام و آرزوی موفقیت
مسائل گروه ها:
هفته ی اول
جمعه ۱۰ مهر ۱۳۸۸
گروه ۱: همه ی جواب های معادله ی زیر را به دست آورید:

گروه ۲: نامعادله ی زیر را حل کنید:

گروه ۳: نامعادله ی زیر را حل کنید:

گروه 4: بازه ی 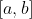 را به سه قسمت مساوی تقسیم می کنیم و نقاطی که این پاره خط را به سه قسمت مساوی تقسیم می کنند x و y می نامیم. x و y را بر حسب a و b بنویسید.
را به سه قسمت مساوی تقسیم می کنیم و نقاطی که این پاره خط را به سه قسمت مساوی تقسیم می کنند x و y می نامیم. x و y را بر حسب a و b بنویسید.
گروه 5: نامعادله ی زیر را حل کنید:
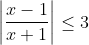
گروه 6: نامعادله ی زیر را حل کنید:

هفته ی دوم
جمعه ۱۷ مهر ۱۳۸۸
گروه 1: اگر =\frac{x-1}{x+1}) ثابت کنید
ثابت کنید ))\cdot&space;f(x)=-1) .
.
گروه 2: اگر تابع f در شرط =x^2) صدق کند، (f(x را بیابید.
صدق کند، (f(x را بیابید.
گروه ۳: اگر =ax^2+bx+c) ثابت کنید
ثابت کنید
.-3f(x+2)+3f(x+1)=f(x))
گروه ۴: فرض کنید دنباله ی  تصاعد حسابی باشد. ثابت کنید که اگر
تصاعد حسابی باشد. ثابت کنید که اگر =ax+b) ، آن گاه دنباله ی
، آن گاه دنباله ی \right&space;\}) نیز یک تصاعد حسابی است.
نیز یک تصاعد حسابی است.
گروه ۵: فرض کنید دنباله ی  تصاعد هندسی باشد. ثابت کنید که اگر
تصاعد هندسی باشد. ثابت کنید که اگر =a^x) (a عددی مثبت و مخالف1 است)، آن گاه دنباله ی
(a عددی مثبت و مخالف1 است)، آن گاه دنباله ی \right&space;\}) نیز یک تصاعد هندسی است.
نیز یک تصاعد هندسی است.
گروه 6: اگر =\frac{1}{2}\left&space;(&space;a^x+a^{-x}&space;\right&space;)) (a عددی مثبت و مخالف1 است)، ثابت کنید
(a عددی مثبت و مخالف1 است)، ثابت کنید
.+f(x-y)=2f(x)f(y))
هفته ی سوم
جمعه ۲۴ مهر ۱۳۸۸
گروه 1: اگر =ax+b) ، آن گاه
، آن گاه ))),f(f(f(x))),f(f(x))) را محاسبه کنید. اگر n بار این کار را انجام دهیم، فرمول دقیق را به دست آورید.
را محاسبه کنید. اگر n بار این کار را انجام دهیم، فرمول دقیق را به دست آورید.
گروه 2: مساله ی گروه 1 را با تابع زیر انجام دهید:
=\frac{x}{\sqrt{1+x^2}})
گروه 3: فرض کنید
.=x^3+\frac{1}{x^3},\,\,\,g(x+\frac{1}{x})=x^4+\frac{1}{x^4})
ضابطه ی دو تابع f و g را به طور صریح بیابید.
گروه ۴: اگر =x^2+2x+2) ، آن گاه دو تابع g چنان بیابید که داشته باشیم
، آن گاه دو تابع g چنان بیابید که داشته باشیم
.)=x^2-4x+5)
گروه 5: اگر =log(x+\sqrt{x^2-1})) ، ثابت کنید
، ثابت کنید
&space;&=2f(x)\,\,\,(x>0)&space;\\&space;f(4x^3-3x)&=&space;3f(x)\,\,\,(\left&space;|&space;x&space;\right&space;|\geq\frac{1}{2}).&space;\end{align*})
گروه 6: برای هر عدد طبیعی n، تابع f را به صورت زیر تعریف می کنیم:
=1,\,\,\,f(n)=f(n-1)+a^n\,\,\,(n\geq&space;2))
در این صورت (f(n بیابید.
هفته ی چهارم
چهارشنبه ۲۹ مهر ۱۳۸۸
گروه 1: فرض کنید =sin(x)-cos(x)) . ثابت کنید
. ثابت کنید >0) . (توجه کنید که در این جا منظور از 1، همان 1 رادیان است.)
. (توجه کنید که در این جا منظور از 1، همان 1 رادیان است.)
گروه 2: تابع =\frac{4-x}{2x-4}) را در نظر بگیرید. ثابت کنید که مقدار ثابتی مانند
را در نظر بگیرید. ثابت کنید که مقدار ثابتی مانند  وجود دارد که
وجود دارد که \cdot&space;f(\alpha&space;-x)) مقدار ثابتی است.
مقدار ثابتی است.
گروه 3: تابع زیر را در نظر بگیرید:
=\frac{a(x-b)(x-c)}{(a-b)(a-c)}+\frac{b(x-c)(x-a)}{(b-c)(b-a)}+\frac{c(x-a)(x-b)}{(c-a)(c-b)})
مقادیر ,f(a)) و
و ) را محاسبه کنید و سپس با توجه به عبارت
را محاسبه کنید و سپس با توجه به عبارت -x) ،نتیجه بگیرید که
،نتیجه بگیرید که =x) .
.
گروه ۴: فرض کنید n عددی فرد باشد و  . تابع f را چنان بیابید که ضابطه ی آن در رابطه ی زیر صدق کند:
. تابع f را چنان بیابید که ضابطه ی آن در رابطه ی زیر صدق کند:
.+f(-x^n)=bx)
گروه 5: اگر \cdot&space;sin(x)+f(-x)\cdot&space;cos(x)=x) ، در این صورت
، در این صورت ) را بیابید.
را بیابید.
گروه 6: فرض کنید =1+x+x^2+\cdots+x^8) . مقدار
. مقدار \cdot&space;f(-\sqrt{2})) را به طور دقیق محاسبه کنید.
را به طور دقیق محاسبه کنید.
هفته ی پنجم
پنج شنبه 7 آبان ۱۳۸۸
برد توابع زیر را به دست آورید (شماره ی مساله، مربوط به شماره ی گروه است):
-
-
-
-
-
-
هفته ی ششم
جمعه ۲۲ آبان ۱۳۸۸
دامنه ی توابع زیر را به دست آورید (شماره ی مساله، مربوط به شماره ی گروه است):
-
-
-
-
-
-
هفته ی هفتم
پنج شنبه ۵ آذر ۱۳۸۸
(شماره ی مساله، مربوط به شماره ی گروه است):
۱. تابع f روی اعداد گویا به صورت زیر تعریف شده است:
.=f(x)+f(y))
ثابت کنید که برای هر x داریم: =f(1)\cdot&space;f(x))
2. فرض کنید =x^2-1) . درباره ی نقاط برخورد تابع
. درباره ی نقاط برخورد تابع  با محور طول ها تحقیق کنید.
با محور طول ها تحقیق کنید.
3. ثابت کنید معادله ی زیر، ریشه ی حقیقی ندارد:

4. اگر b ،a و c اعداد صحیح فرد باشند، ثابت کنید معادله ی 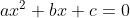 ریشه ی گویا ندارد.
ریشه ی گویا ندارد.
5. به ازای چه مقداری از m، معادله ی  ، دو ریشه ی حقیقی و معکوس هم دارد؟
، دو ریشه ی حقیقی و معکوس هم دارد؟
6. به ازای چه مقداری از m، عدد  میانگین دو ریشه ی حقیقی معادله ی درجه ی دوم زیر است؟
میانگین دو ریشه ی حقیقی معادله ی درجه ی دوم زیر است؟
x^2-3x+m=0)
هفته ی هشتم
پنج شنبه ۱۲ آذر ۱۳۸۸
(شماره ی مساله، مربوط به شماره ی گروه است):
1. بین p و q و 'p و 'q که  ، چه رابطه ای برقرار باشد تا دو معادله ی زیر، یک ریشه ی مشترک داشته باشند؟
، چه رابطه ای برقرار باشد تا دو معادله ی زیر، یک ریشه ی مشترک داشته باشند؟
.
2. m را چنان بیابید که یکی از ریشه های معادله ی  دو برابر یکی از ریشه های
دو برابر یکی از ریشه های x+3=0) باشد.
باشد.
3. فرض کنید  و
و  ، ریشه های معادله ی
، ریشه های معادله ی  باشند. مقدار
باشند. مقدار  را بیابید.
را بیابید.
۴. معادله ای تشکیل دهید که ریشه های آن، توان چهارم ریشه های معادله ی زیر باشد:
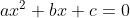
۵. فرض کنید  و
و  ، ریشه های معادله ی
، ریشه های معادله ی 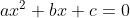 باشند. ثابت کنید که b و c ریشه های معادله ی
باشند. ثابت کنید که b و c ریشه های معادله ی x-\alpha\beta(\alpha+\beta)=0) هستند.
هستند.
6. فرض کنید فرض کنید  و
و  ، ریشه های معادله ی
، ریشه های معادله ی  باشند. p را به گونه ای بیابید که
باشند. p را به گونه ای بیابید که  .
.
هفته ی نهم
پنج شنبه ۱۹ آذر ۱۳۸۸
(شماره ی مساله، مربوط به شماره ی گروه است):
۱. ) را چند جمله ای از درجه ی ۴ بگیرید. فرض کنید
را چند جمله ای از درجه ی ۴ بگیرید. فرض کنید ) بر
بر 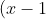^2) و
و ) بر
بر ^3) بخش پذیر باشد و
بخش پذیر باشد و =81) . با شرایط ذکر شده،
. با شرایط ذکر شده،) را بیابید.
را بیابید.
2. اگر +2f(x)=x^3) ، با قی مانده ی تقسیم
، با قی مانده ی تقسیم ) بر
بر 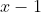 را به دست آورید.
را به دست آورید.
3. مقادیر a و b را چنان بیابید که عبارت  بر عبارت
بر عبارت  بخش پذیر باشد.
بخش پذیر باشد.
4. ثابت کنید که اگر باقی مانده ی تقسیم چند جمله ای درجه ی 2 ی ) بر
بر 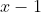 و
و 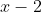 و
و 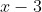 به ترتیب 0 و 1 و 4 باشد، باید
به ترتیب 0 و 1 و 4 باشد، باید =(x-1)^2) .
.
5. در تقسیم  بر
بر  و
و 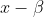 به ترتیب باقی مانده های
به ترتیب باقی مانده های  و
و  به دست آمده است. دو رابطه ی زیر را ثابت کنید:
به دست آمده است. دو رابطه ی زیر را ثابت کنید:
,\,\,\,(\alpha+\beta)(\alpha\beta+1)=q)
6. ثابت کنید که اگر چند جمله ای  بر
بر 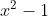 قابل قسمت باشد، بر
قابل قسمت باشد، بر 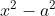 هم قابل قسمت است.
هم قابل قسمت است.
هفته ی دهم
پنج شنبه ۲۶ آذر ۱۳۸۸
(شماره ی مساله، مربوط به شماره ی گروه است):
۱. فرض کنید =x+\sqrt{x^2+1}) ؛ در این صورت، ضابطه ی
؛ در این صورت، ضابطه ی ) را به طور دقیق، به دست آورید.
را به طور دقیق، به دست آورید.
2. آیا می توان گفت که اگر تابعی فرد و معکوس پذیر باشد، معکوس آن نیز تابعی فرد است؟ اگر این ادعا درست است، آن را ثابت کنید و اگر نیست، مثال نقضی برای آن بیاورید.
3. ثابت کنید تابع زیر، یک به یک است:

4. ثابت کنید تابع زیر، یک به یک است و معکوس آن را به دست آورید:
=x+\frac{1}{x}\,\,\,\,\,(x\geq 1))
5. ثابت کنید تابع =x|x|) ، یک به یک است و معکوس آن را به دست آورید.
، یک به یک است و معکوس آن را به دست آورید.
6. آیا می توان گفت که اگر f تابعی با دامنه ی  باشد، در این صورت
باشد، در این صورت +f(-x)) معکوس ناپذیر است؟ اگر این ادعا درست است، آن را ثابت کنید و اگر نیست، مثال نقضی برای آن بیاورید.
معکوس ناپذیر است؟ اگر این ادعا درست است، آن را ثابت کنید و اگر نیست، مثال نقضی برای آن بیاورید.
موفق و پیروز باشید.

 را محاسبه کنیم.
را محاسبه کنیم. (ثابت کنید). اگر
(ثابت کنید). اگر  آنگاه
آنگاه  و اگر
و اگر  آنگاه
آنگاه  . به تصاویر زیر توجه کنید:
. به تصاویر زیر توجه کنید:
 برابر است با
برابر است با  زیرا با توجه به نکات بالا
زیرا با توجه به نکات بالا  .
. برابر است با R .
برابر است با R . اعمال زیر را انجام می دهیم:
اعمال زیر را انجام می دهیم:
 .
.
 ، آنگاه
، آنگاه  .
.
 . (دقت کنید که اگر قرار دهیم
. (دقت کنید که اگر قرار دهیم  ، آنگاه y=0.) می توان نوشت:
، آنگاه y=0.) می توان نوشت:  . در نتیجه
. در نتیجه  . چون دامنه ی تابع
. چون دامنه ی تابع  برابر است با R و چون
برابر است با R و چون  برابر خواهد بود.
برابر خواهد بود.


 . اما y>0 ، در نتیجه برد تابع f برابر است با
. اما y>0 ، در نتیجه برد تابع f برابر است با  .
.


 و لذا
و لذا  ؛ در نتیجه خواهیم داشت:
؛ در نتیجه خواهیم داشت:  . (توجه کنید که اگر x=-1 آنگاه y=1 و اگر x=1 آنگاه y=-1.)
. (توجه کنید که اگر x=-1 آنگاه y=1 و اگر x=1 آنگاه y=-1.)
 و لذا
و لذا 


 . بنابراین خواهیم داشت:
. بنابراین خواهیم داشت:  . (روش دیگر برای پیدا کردن برد این تابع، استفاده از مشتق است که به آن نمی پردازیم.)
. (روش دیگر برای پیدا کردن برد این تابع، استفاده از مشتق است که به آن نمی پردازیم.)
 . توجه کنید که اگر
. توجه کنید که اگر  ، آنگاه
، آنگاه  .
. و برد توابع (tan(x و (cot(x برابر است با R. (چرا؟)
و برد توابع (tan(x و (cot(x برابر است با R. (چرا؟)
 . چون
. چون  بنابر این
بنابر این  و در نتیجه برای هر
و در نتیجه برای هر  خواهیم داشت
خواهیم داشت  ، پس
، پس  .
.
 . اما بنابر نکته ی 4 می توان نوشت:
. اما بنابر نکته ی 4 می توان نوشت:  ، در نتیجه
، در نتیجه  ، پس
، پس  . (توجه کنید که در این مثال و بعضی مثالهای بالا، به طور مخفیانه از قضیه ی مقدار میانگین استفاده شده است که این قضیه را در پیش دانشگاهی خواهید دید.)
. (توجه کنید که در این مثال و بعضی مثالهای بالا، به طور مخفیانه از قضیه ی مقدار میانگین استفاده شده است که این قضیه را در پیش دانشگاهی خواهید دید.) و
و  ، بنابر این
، بنابر این  و در نتیجه
و در نتیجه  .
.  برابر با 2 یا 2- نیست و لذا
برابر با 2 یا 2- نیست و لذا  (دقت کنید)! در واقع به وسیله ی استدلال بالا فقط می توان نتیجه گرفت که
(دقت کنید)! در واقع به وسیله ی استدلال بالا فقط می توان نتیجه گرفت که . همین ریزه کاریهاست که محاسبه ی برد بعضی از توابع را مشکل می کند.
. همین ریزه کاریهاست که محاسبه ی برد بعضی از توابع را مشکل می کند.
 . در حالت کلی برد تابع
. در حالت کلی برد تابع  زیر مجموعه ای از
زیر مجموعه ای از 
 همواره مثبت و صورت کسر از مخرج آن کمتر است. بنابر این
همواره مثبت و صورت کسر از مخرج آن کمتر است. بنابر این  و درنتیجه بنابر خواص جزءصحیح برای هر
و درنتیجه بنابر خواص جزءصحیح برای هر  .
. . چون
. چون  بنابر این
بنابر این  . در نتیجه
. در نتیجه  .
.

 .
.
 . به عنوان مثال دامنه ی همه ی 5 تابع زیر R است:
. به عنوان مثال دامنه ی همه ی 5 تابع زیر R است:






 . اما x=-1 تنها ریشه مخرج است، در نتیجه
. اما x=-1 تنها ریشه مخرج است، در نتیجه  .
. برابر نیست. (چرا؟)
برابر نیست. (چرا؟)
 . بنابر این با محاسبه ی اشتراک R و
. بنابر این با محاسبه ی اشتراک R و  .
.


 است. با تعیین علامت تابع زیر رادیکال، مجموعه ی همه اعدادی که این تابع را نامنفی می کند عبارت است از
است. با تعیین علامت تابع زیر رادیکال، مجموعه ی همه اعدادی که این تابع را نامنفی می کند عبارت است از  . حال با اشتراک
. حال با اشتراک  .
. با دامنه ی تابع
با دامنه ی تابع  برابر است و در نتیجه دامنه ی f برابر است با
برابر است و در نتیجه دامنه ی f برابر است با  به وضوح R است. در حالت کلی، دامنه ی
به وضوح R است. در حالت کلی، دامنه ی (قدر مطلق (g(x ) برابر است با دامنه ی تابع (g(x . به طور مثال دامنه ی تابع
(قدر مطلق (g(x ) برابر است با دامنه ی تابع (g(x . به طور مثال دامنه ی تابع  ( قدر مطلق
( قدر مطلق  برابر است با R . در حالت کلی، دامنه
برابر است با R . در حالت کلی، دامنه  (جزء صحیح (h(x ) برابر است با دامنه ی تابع (h(x . به طور مثال دامنه ی تابع
(جزء صحیح (h(x ) برابر است با دامنه ی تابع (h(x . به طور مثال دامنه ی تابع  ( جزء صحیح
( جزء صحیح  برابر است با اعداد حقیقی مثبت. (توجه کنید که a عددی مثبت و مخالف 1 است.) در حالت کلی، دامنه
برابر است با اعداد حقیقی مثبت. (توجه کنید که a عددی مثبت و مخالف 1 است.) در حالت کلی، دامنه  ( a عددی مثبت و مخالف 1 ) برابر است با
( a عددی مثبت و مخالف 1 ) برابر است با  . به دو مثال زیر توجه کنید:
. به دو مثال زیر توجه کنید:
 است که به ازای آن x ها داشته باشیم
است که به ازای آن x ها داشته باشیم  . چون دامنه ی تابع
. چون دامنه ی تابع  .
.
 تغییر کند. از طرف دیگر عبارت روبروی لگاریتم نیز باید عددی مثبت باشد (این عبارت را تعیین علامت کنید). بنابر این
تغییر کند. از طرف دیگر عبارت روبروی لگاریتم نیز باید عددی مثبت باشد (این عبارت را تعیین علامت کنید). بنابر این  .
. برابر است با R (توجه کنید که a عددی مثبت و مخالف 1 است). در حالت کلی، دامنه
برابر است با R (توجه کنید که a عددی مثبت و مخالف 1 است). در حالت کلی، دامنه  (a به توان (g(x ) برابر است با دامنه ی تابع (g(x . به طور مثال دامنه ی تابع
(a به توان (g(x ) برابر است با دامنه ی تابع (g(x . به طور مثال دامنه ی تابع  ( 2 به توان
( 2 به توان  .
. .
.  ) و (Arccos(x (یا
) و (Arccos(x (یا  ) برابر است با
) برابر است با  ) و تابع (Arccot(x (یا
) و تابع (Arccot(x (یا  ) برابر است با R.
) برابر است با R. 





 (بنابر این دامنه ی این تابع، مجموعه ی تک عنصری است.)
(بنابر این دامنه ی این تابع، مجموعه ی تک عنصری است.)
 (بنابر این دامنه ی این تابع، تهی است. چنین توابعی را معمولاً تابع تهی گوییم.)
(بنابر این دامنه ی این تابع، تهی است. چنین توابعی را معمولاً تابع تهی گوییم.)


 خواهد بود.
خواهد بود. .
.
 یک تابع است.)
یک تابع است.) یا
یا  و می خوانیم f تابعی با دامنه ی D و برد R است که هر x از D را به (f(x از R تصویر می کند. (در واقع خروجی x از دستگاه f را (f(x می نامیم.) به
و می خوانیم f تابعی با دامنه ی D و برد R است که هر x از D را به (f(x از R تصویر می کند. (در واقع خروجی x از دستگاه f را (f(x می نامیم.) به  یا
یا  ضابطه یا قانون تابع f گوییم. دامنه ی f را گاهی با
ضابطه یا قانون تابع f گوییم. دامنه ی f را گاهی با  و برد f را گاهی با
و برد f را گاهی با  نمایش می دهیم.
نمایش می دهیم. تابعی است که هر عنصر مجموعه ی
تابعی است که هر عنصر مجموعه ی را ابتدا در ۲ ضرب و سپس با ۱ جمع می کند. به طور مثال
را ابتدا در ۲ ضرب و سپس با ۱ جمع می کند. به طور مثال  و
و  ( یعنی تصویر ۰ تحت تابع f عدد ۱ و تصویر عدد 1- تحت تابع f عدد 1- است) و ضابطه ی این تابع
( یعنی تصویر ۰ تحت تابع f عدد ۱ و تصویر عدد 1- تحت تابع f عدد 1- است) و ضابطه ی این تابع  .
. تابعی است که به هر عدد مثبت r، عدد
تابعی است که به هر عدد مثبت r، عدد  را منسوب می کند. به طور خلاصه می توان نوشت:
را منسوب می کند. به طور خلاصه می توان نوشت:  که
که  ؛ یعنی ضابطه ی S با دامنه ی
؛ یعنی ضابطه ی S با دامنه ی  عبارت است از
عبارت است از  است، زیرا
است، زیرا

 :
:
 را برای تابع های زیر پیدا کنید(توجه کنید که در این مساله، h مخالف صفر است):
را برای تابع های زیر پیدا کنید(توجه کنید که در این مساله، h مخالف صفر است):







 و
و  صدق می کنند که دارای مولفه های اول مساوی هستند، یعنی
صدق می کنند که دارای مولفه های اول مساوی هستند، یعنی  . ثابت می کنیم مولفه های دوم نیز برابرند؛ یعنی ثابت می کنیم
. ثابت می کنیم مولفه های دوم نیز برابرند؛ یعنی ثابت می کنیم  .
.


 را به صورت زوجهای مرتب بنویسید. آیا f یک تابع است؟چرا؟
را به صورت زوجهای مرتب بنویسید. آیا f یک تابع است؟چرا؟ یک تابع باشد، مقدار k را محاسبه کنید.
یک تابع باشد، مقدار k را محاسبه کنید.






 یا
یا یا
یا




 . بنابر این
. بنابر این
 . بنابر این
. بنابر این 

 را حل کنید. )
را حل کنید. ) باشد که مجموع همه سطرهای آنها برابر 1 است. ثابت کنید که S نسبت به ضرب بسته است.
باشد که مجموع همه سطرهای آنها برابر 1 است. ثابت کنید که S نسبت به ضرب بسته است.

 اصم است.
اصم است.


 که
که  ، ثابت کنید
، ثابت کنید  عددی صحیح است.
عددی صحیح است.
 و
و  اعداد صحیح هستند که نتیجه را ثابت می کند.
اعداد صحیح هستند که نتیجه را ثابت می کند.  از اعداد صحیح را بیابید به طوری که
از اعداد صحیح را بیابید به طوری که  .
. وجود دارد. به ویژه فرض کنید
وجود دارد. به ویژه فرض کنید  نظیر شود. به سادگی دیده می شود که این، تناظری یک به یک است. به عبارت دیگر هر عضو مجموعه مورد نظر ما، دقیقاً با یکی از زیر مجموعه های چهارتایی
نظیر شود. به سادگی دیده می شود که این، تناظری یک به یک است. به عبارت دیگر هر عضو مجموعه مورد نظر ما، دقیقاً با یکی از زیر مجموعه های چهارتایی  است.
است.


 برای n=1 و n=4 مجذور کامل داریم. اگر
برای n=1 و n=4 مجذور کامل داریم. اگر  :
:






















 دقیقاً یک ریشه حقیقی دارد و اگر x0 این ریشه باشد آنگاه
دقیقاً یک ریشه حقیقی دارد و اگر x0 این ریشه باشد آنگاه  .
. . با توجه به مشتق، این تابع اکیداً صعودی و لذا یک به یک و پوشاست و لذا دقیقاً یک x0 چنان موجود است که
. با توجه به مشتق، این تابع اکیداً صعودی و لذا یک به یک و پوشاست و لذا دقیقاً یک x0 چنان موجود است که  . اما به راحتی می توان دید که
. اما به راحتی می توان دید که  . حال فرض کنید g معکوس تابع f باشد. پس g نیز اکیداً صعودی است. با اثر دادن g به طرفین نامساوی بالا عبارت
. حال فرض کنید g معکوس تابع f باشد. پس g نیز اکیداً صعودی است. با اثر دادن g به طرفین نامساوی بالا عبارت 

 .
.

 و برای
و برای  به صورت بازگشتی تعریف می کنیم:
به صورت بازگشتی تعریف می کنیم:

 که
که  وجود دارد به طوری که
وجود دارد به طوری که  . به ازای این
. به ازای این 
 . حال می توان نوشت:
. حال می توان نوشت:
 و پرانتز به 1 نزدیک می شود و لذا جواب حد برابر است با
و پرانتز به 1 نزدیک می شود و لذا جواب حد برابر است با 






 . عبارات زیر را بر حسب a به دست آورید:
. عبارات زیر را بر حسب a به دست آورید:

 است.
است. صدق می کنند.
صدق می کنند.










 حال فرض کنید x مثبت باشد. عبارت
حال فرض کنید x مثبت باشد. عبارت  را محاسبه کنید و به دست آورید:
را محاسبه کنید و به دست آورید:
 .
.

 را قرار دهید. با محاسبه ای مختصر به تابع سمت راست می رسیم. در نتیجه از حل معادله
را قرار دهید. با محاسبه ای مختصر به تابع سمت راست می رسیم. در نتیجه از حل معادله  تنها جواب معادله
تنها جواب معادله  به دست می آید.
به دست می آید.

 . حال f را 1977 بار با خودش ترکیب کنید و حاصل را تابع g بنامید.
. حال f را 1977 بار با خودش ترکیب کنید و حاصل را تابع g بنامید.  را حساب کنید.
را حساب کنید.














































 لذا
لذا


 و T2 مثلثی با زوایای حاده باشد. آیا می توان نتیجه گرفت که
و T2 مثلثی با زوایای حاده باشد. آیا می توان نتیجه گرفت که  ؟
؟ ،
،  و
و  به ترتیب زوایای روبه رو به اضلاع bi , ai و ci باشند. چون
به ترتیب زوایای روبه رو به اضلاع bi , ai و ci باشند. چون  ، بنابر این حداقل یکی از نامساویهای زیر برقرار است:
، بنابر این حداقل یکی از نامساویهای زیر برقرار است:
 . اما
. اما  و اینکه sinx در
و اینکه sinx در  صعودی است. لذا
صعودی است. لذا  .
.











 . ثابت کنید:
. ثابت کنید:
 ثابت می کنیم:
ثابت می کنیم: 

 . در این صورت مقدار
. در این صورت مقدار  را به دست آورید.
را به دست آورید.


 مساوی یک عدد صحیح باشد.
مساوی یک عدد صحیح باشد. . حال با توجه به اینکه k نمی تواند مساوی 1 باشد، طرف سمت چپ، منفی است و لذا k برابر است با 2 یا 3. با بررسی مختصر می توان دید که باید b=2.
. حال با توجه به اینکه k نمی تواند مساوی 1 باشد، طرف سمت چپ، منفی است و لذا k برابر است با 2 یا 3. با بررسی مختصر می توان دید که باید b=2.
 برای همه مقادیر صحیح
برای همه مقادیر صحیح  یک کسر ساده نشدنی است، یعنی برزگترین مقسوم علیه مشترک صورت و مخرج، ۱ است.
یک کسر ساده نشدنی است، یعنی برزگترین مقسوم علیه مشترک صورت و مخرج، ۱ است.
 آن است که
آن است که  یا
یا  .
. را به عوامل ضرب تجزیه کنید.
را به عوامل ضرب تجزیه کنید. ، مقدار عبارت زیر را به دست آورید:
، مقدار عبارت زیر را به دست آورید:

 جواب مساله است.
جواب مساله است.
 است.
است.
 . با در نظر گرفتن ترتیب عاملهای جمع، به چند طریق می توان عدد n را به شکل مجموعی از m عدد طبیعی نوشت؟
. با در نظر گرفتن ترتیب عاملهای جمع، به چند طریق می توان عدد n را به شکل مجموعی از m عدد طبیعی نوشت؟ .
.  . پس
. پس  . بنابر این طول ضلعهای مثلث 4d، 3d و 5d است.
. بنابر این طول ضلعهای مثلث 4d، 3d و 5d است.  یک عدد اول نیست.
یک عدد اول نیست.

